GRM Performance Metrics

The performance of an investment strategy can be measured using a series of basic financial metrics. These industry-standard metrics allow investors to assess both the quality of returns, as well as the amount of risk that a particular strategy has delivered.
We’ve summarized these performance metrics for our Gold Rotation Model (GRM) in the table below. However, unless you happen to be a particularly savvy investor, there’s a good chance you have no idea what all these numbers mean. Not to worry, in this section we’ll break down each of these metrics so that you can get a better understanding of the GRM’s true capabilities.
| Gold Rotation Model (GRM) Performance Metrics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Strategy | Compound Annual Return | Alpha1 | Beta2 | Standard Deviation | Maximum Drawdown | Sharpe Ratio | Sortino Ratio | Treynor Ratio |
| GRM | 6.02% | 2.06% | 0.08 | 11.76% | -25.83% | 0.35 | 0.53 | 0.55 |
| GLD (Gold) | 4.66% | 0.00% | -0.08 | 14.41% | -42.91% | 0.22 | 0.23 | -0.41 |
| Data for 32-Year Period (1991 – 2022) 1 Benchmarked against GLD 2 Benchmarked against the S&P 500 | ||||||||
Compound Annual Return
The compound annual return is the rate of return that an investment strategy has achieved over time. It represents the cumulative effect of a series of gains and losses on an original amount of capital. In the chart below, you can see that the GRM has delivered a higher compound annual return than GLD – the most popular ETF for investing in gold.
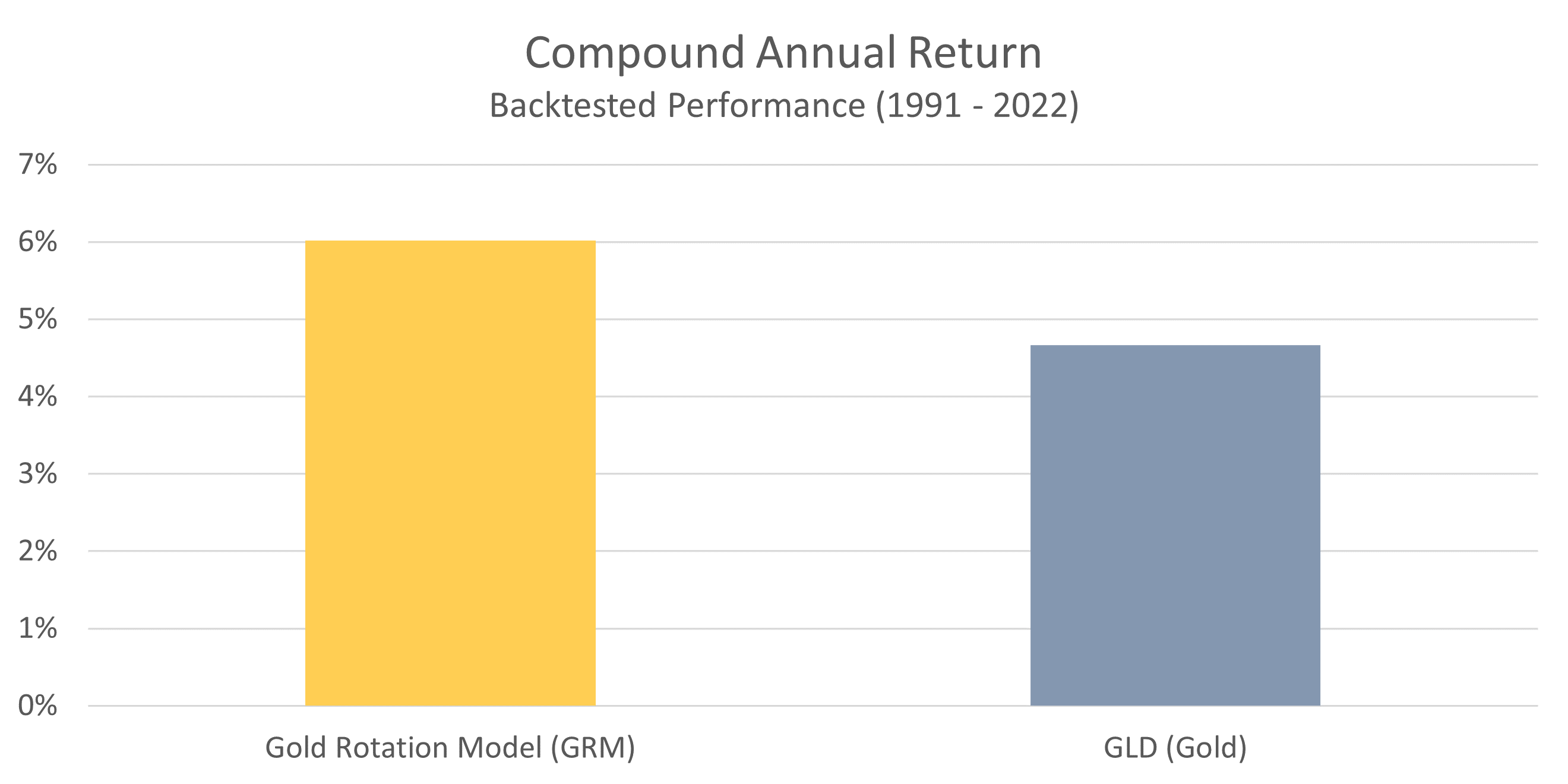
The reason for the GRM’s outperformance stems from the fact that it moves the portfolio in and out of gold based on expected price performance. Gold has experienced a few long, multi-year declines, and avoiding those periods has resulted in higher returns over time. A 1.5% difference may not sound like a lot, but when compounded over time that edge turns out to be quite significant.
Not only has the GRM outperformed a buy-and-hold approach to owning gold, it has done so while exposing the portfolio to less risk. We can see this by examining the three primary metrics that are used to quantify risk: standard deviation, maximum drawdown, and beta.
Standard Deviation
Standard deviation is the most common measure of risk used in the financial industry. It measures the variability of returns over time. The lower the standard deviation, the more consistent the returns are, and therefore the more “safe” a particular strategy is. A higher standard deviation, on the other hand, implies that returns fluctuate wildly from one year to the next.
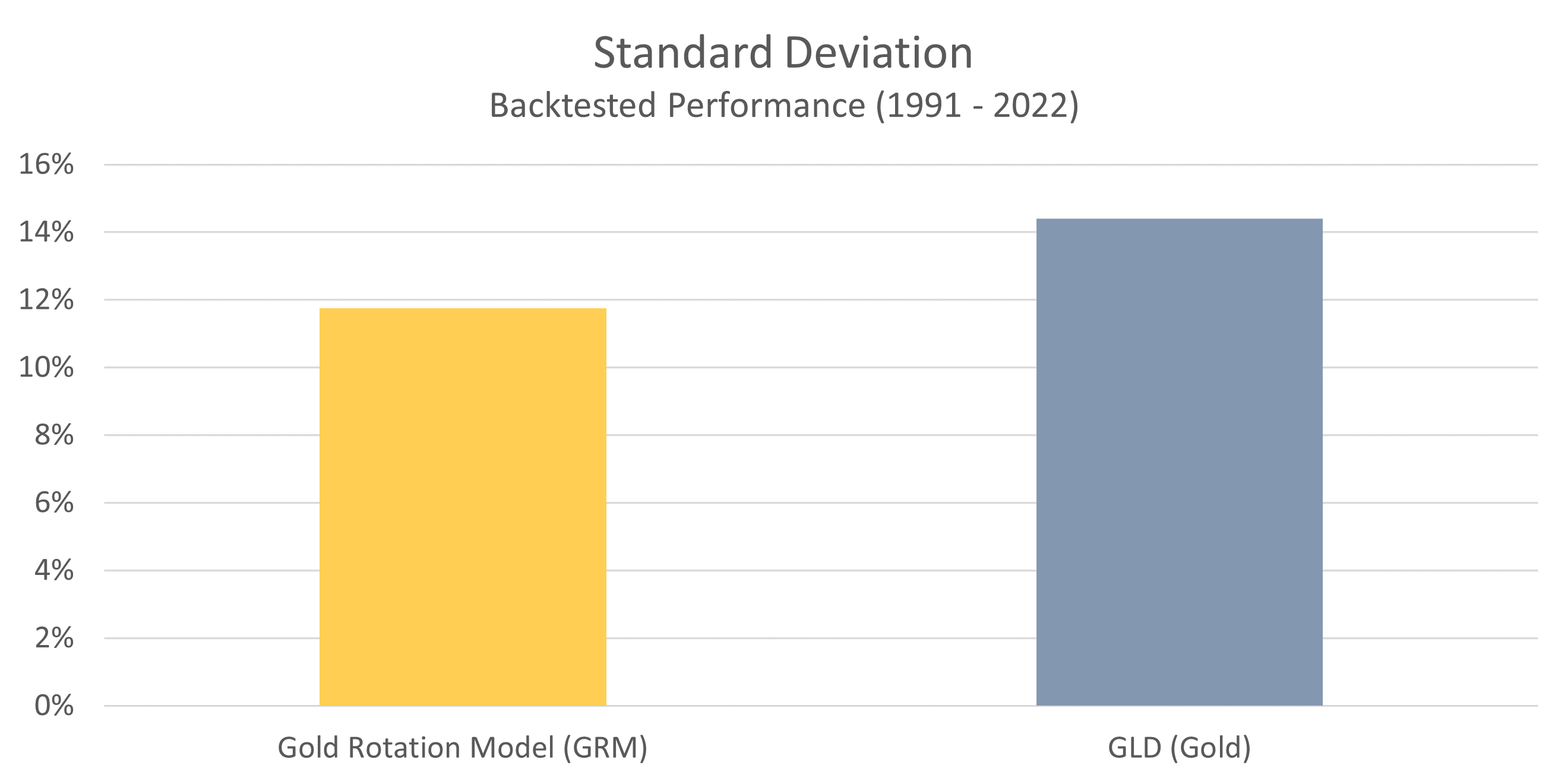
In this chart we can see that the GRM has a lower standard deviation, and thus less volatility (or risk), than simply owning gold for the long haul. Based on this particular metric, the GRM is roughly 20% less volatile than a buy-and-hold approach to owning gold.
Now let’s dig a little deeper and take a look at how elevated levels of volatility can translate into big losses.
Maximum Drawdown
Maximum drawdown is one of the more intuitive ways to measure risk. It looks at the biggest peak-to-trough decline that an investment strategy has ever experienced. It should come as no surprise that the smaller the maximum drawdown, the better. We can see maximum drawdowns for the GRM, as well as GLD, in the chart below.
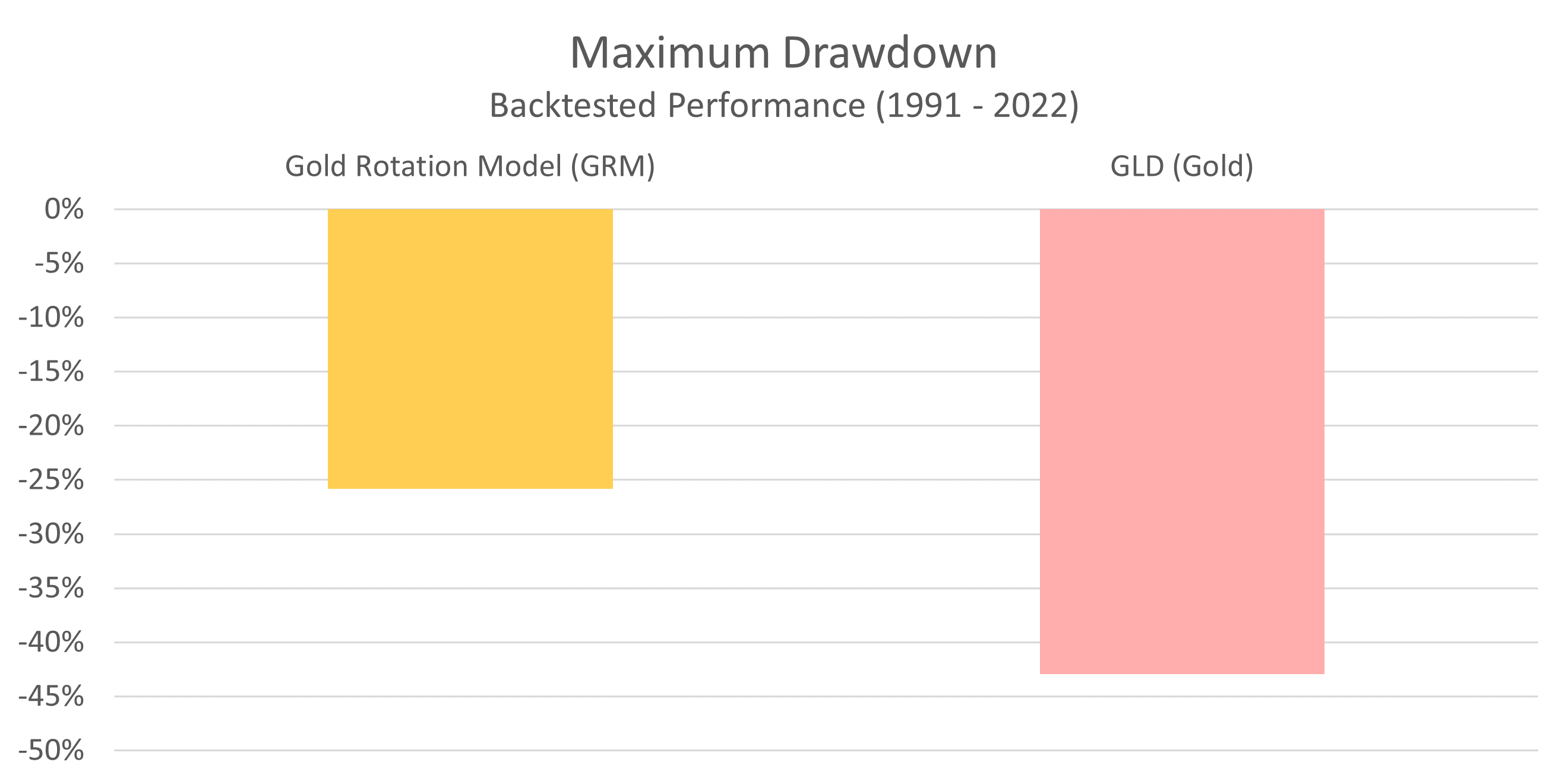
As you can see, the largest peak-to-trough decline the GRM has ever experienced is 25.8%. This compares to a decline of 42.9% in the price of gold itself. By recognizing deteriorating conditions, the GRM has historically been able to sidestep some of the bigger losses that have plagued gold.
Now let’s take a look at our last measure of risk: beta.
Beta
Beta measures the volatility of an investment strategy relative to the S&P 500. A beta of 1 implies the same level of volatility as the S&P 500, while a beta less than 1 implies less risk, and a beta greater than 1 implies more risk. A negative beta indicates an inverse correlation with the S&P 500 (they generally move in opposite directions).
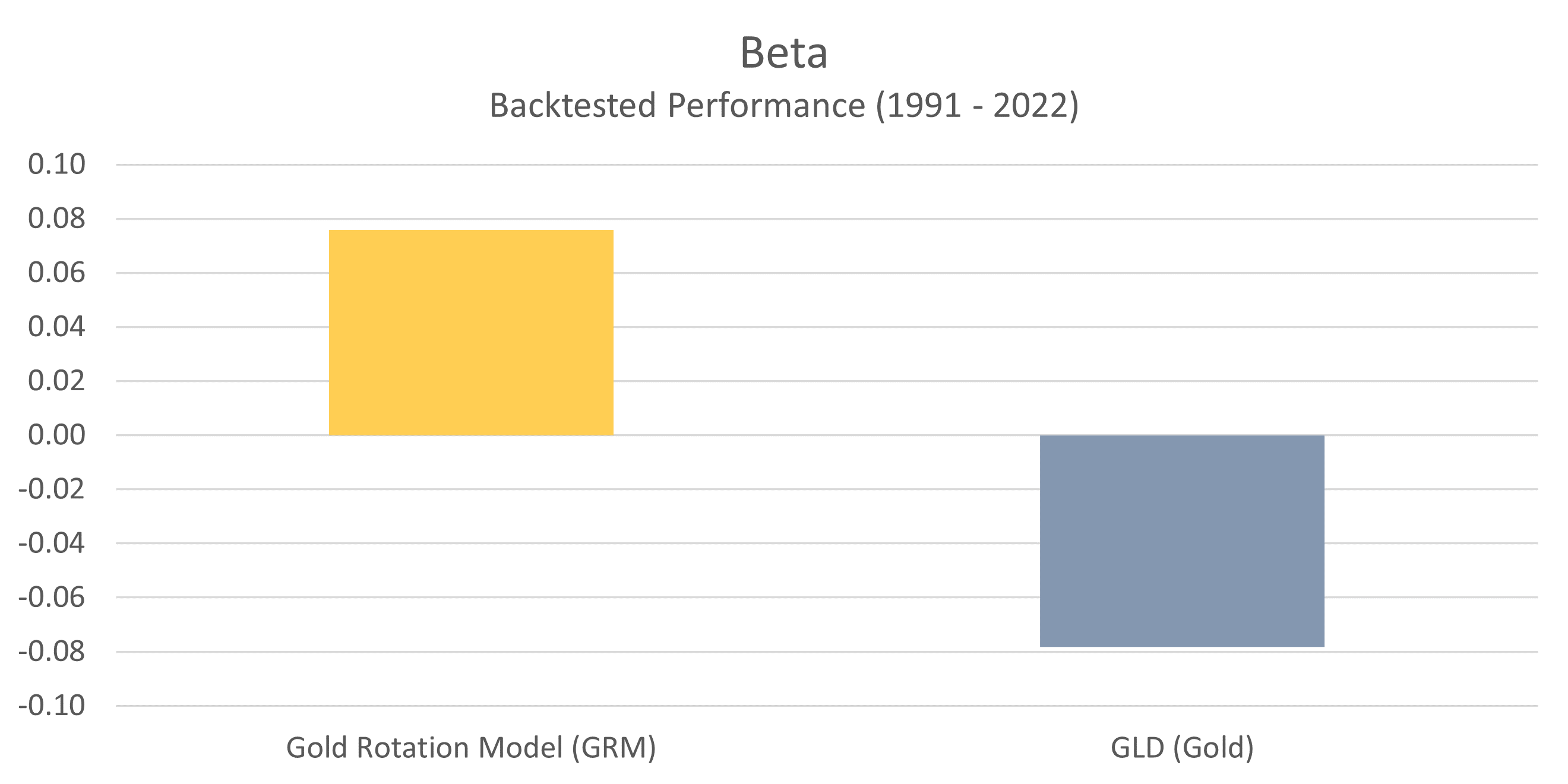
There are two important takeaways from this chart. The first is that when we look at beta from an absolute value perspective, the GRM’s beta is the same as GLD. This implies a similar level of overall volatility.
The other important takeaway has to do with the fact that the GRM’s beta is positive, while GLD’s beta is negative. What this means is that the performance of the GRM has a small positive correlation with the general stock market, while GLD has a slight negative correlation. From this perspective, one could make an argument that owning GLD for the long haul is more ideal, because it has a negative correlation with the equity component of one’s portfolio (thus dragging down total portfolio volatility). That is certainly a valid argument, but the trade-off here is that GLD exhibits lower returns over time.
Now that we’ve covered the metrics that identify both risk (standard deviation, maximum drawdown and beta) as well as returns (compound annual return), we can combine these measures to get a better understanding of risk-adjusted returns. This is considered the holy grail of investing because it represents how efficiently capital is deployed. Anyone can increase returns by taking on more risk, but great investment strategies deliver high returns while taking less risk.
Sharpe Ratio
The Sharpe ratio is the industry standard method for measuring risk-adjusted returns. It looks at the excess return earned in relation to the standard deviation (or volatility) of those returns. With Sharpe ratios, a higher number reflects greater risk-adjusted returns (a good thing).
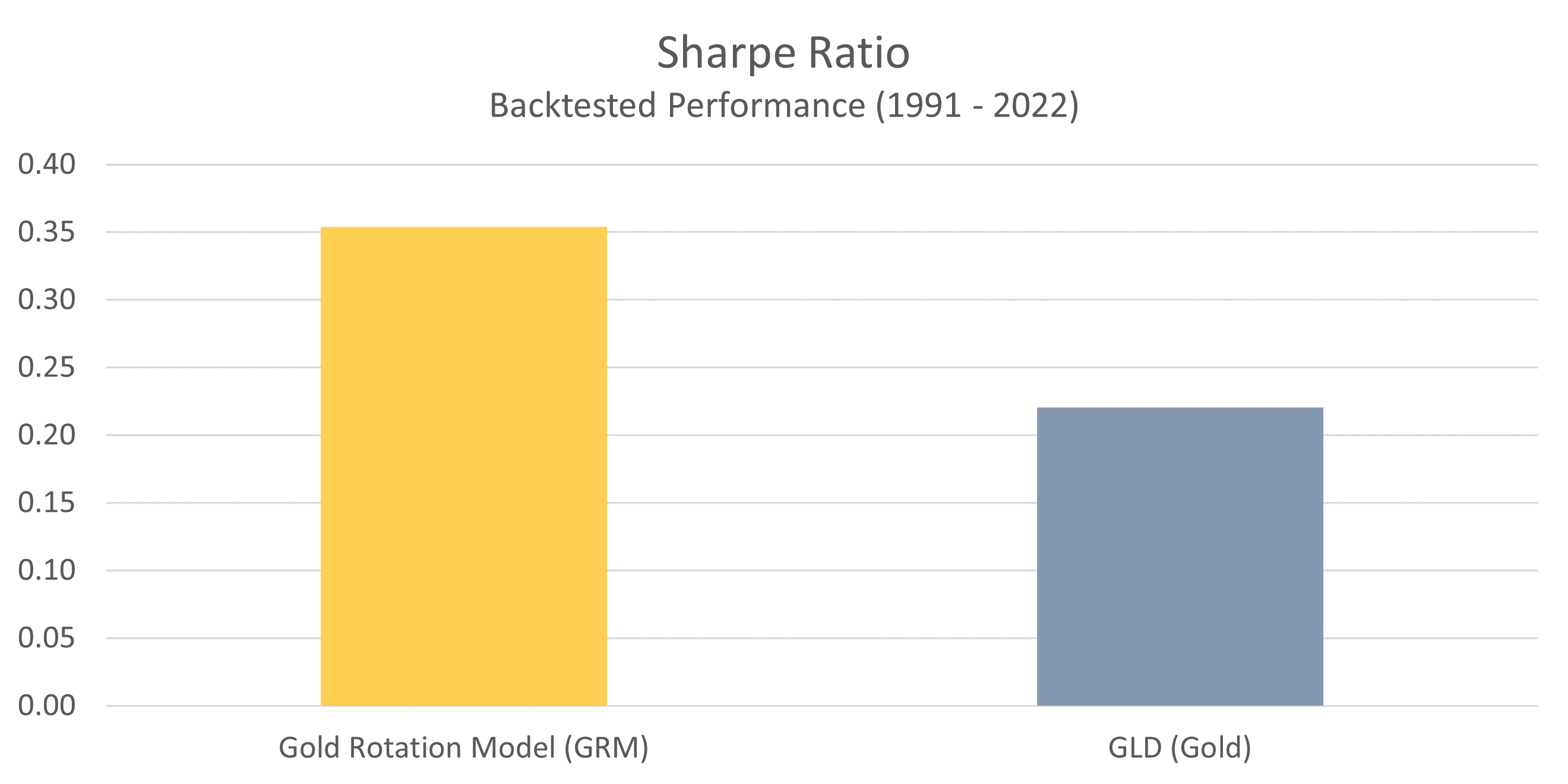
Here we can see that the GRM is able to deliver substantially higher risk-adjusted returns than a buy-and-hold approach to owning gold. Because the GRM has historically generated higher returns on lower volatility, it excels from a risk-adjusted perspective.
When it comes to deciding how to invest, Shape ratios are an extremely important consideration because they demonstrate the true effectiveness of an investment strategy. Looking at returns alone can be misleading because you have no idea how much risk was taken to achieve those returns. The Sharpe ratio illuminates this important information, and gives you a complete picture of the risk-reward profile.
Sortino Ratio
The Sortino ratio is another measure of risk-adjusted returns that is very similar to the Sharpe ratio. However, instead of comparing returns against the total volatility of a portfolio, it compares returns against only the downside volatility (or risk). The assumption here is that volatility to the upside (higher than expected returns) is a good thing, and therefore shouldn’t be penalized.
As with the Sharpe ratio, higher values here represent more effective use of capital.
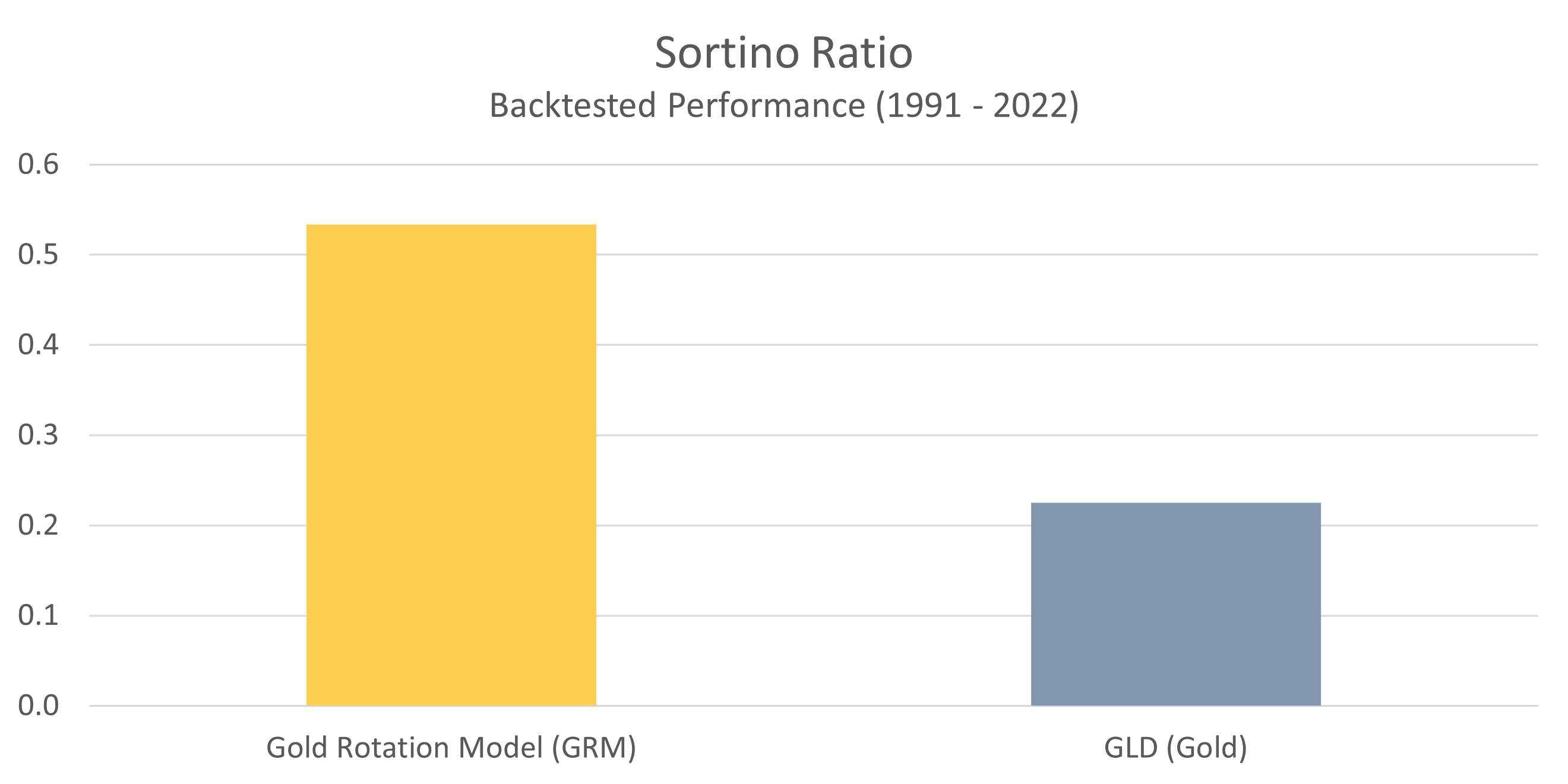
Once again, we can see that the GRM is able to generate significantly higher returns per unit of risk than GLD. The relative outperformance here is more substantial than with the Sharpe ratio because of the fact that upside volatility is not penalized. This means that a significant portion of the GRM’s volatility comes from better than expected returns, as opposed to worse than expected returns.
Treynor Ratio
The last measure of risk-adjusted returns that we’ll look at is called the Treynor ratio, and like the previous two metrics we examined, higher values are better. In this case, the measure of risk used is beta. So we’re looking at the excess returns achieved with regard to overall volatility in relation to the S&P 500.
As you can see, the message here is the same. The GRM has significantly outperformed a buy-and-hold approach to owning gold in terms of risk-adjusted returns.
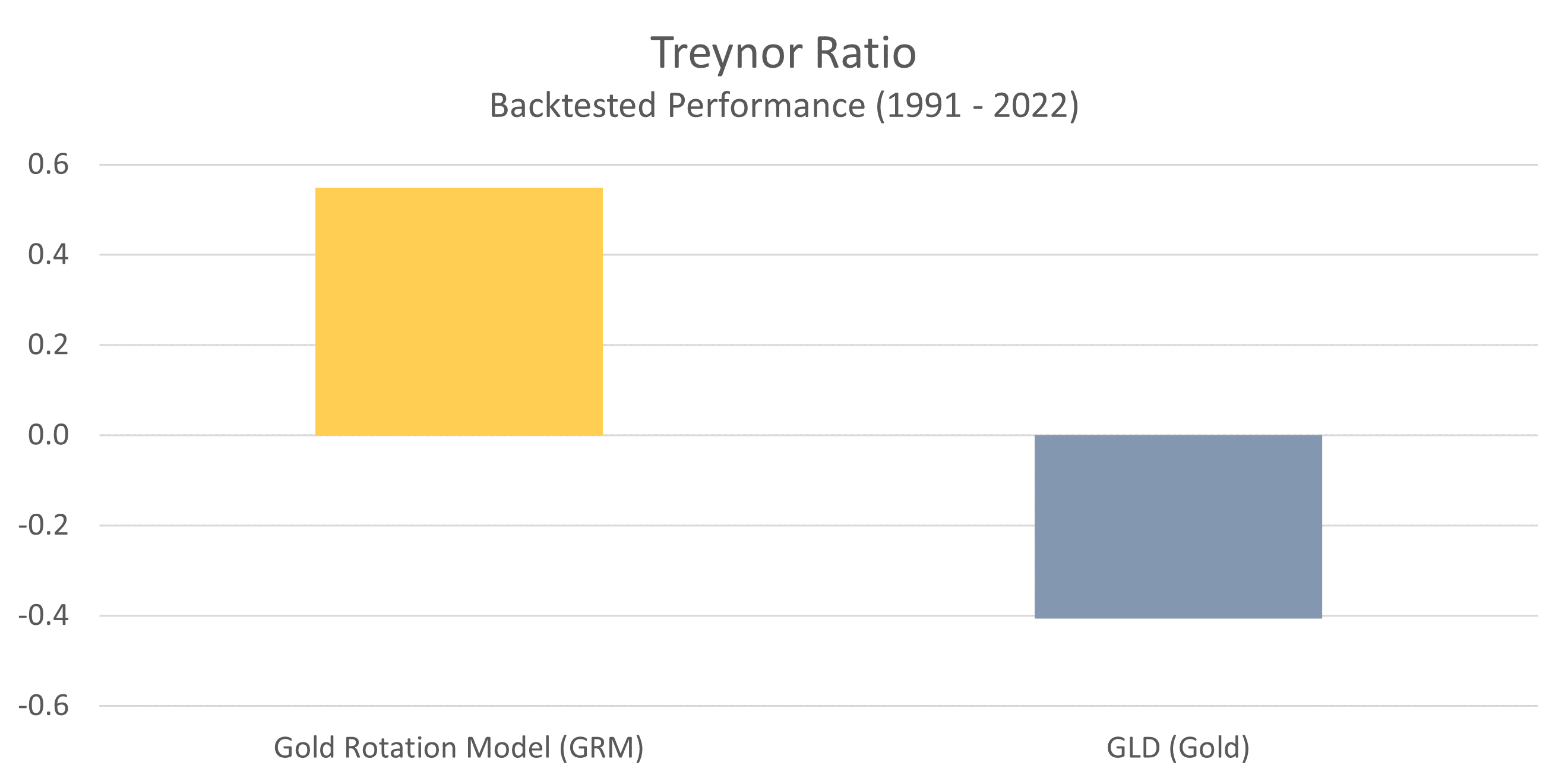
In case you’re wondering why GLD has a negative value here, it’s because the Treynor ratio looks at excess returns in relation to beta, and GLD has a negative beta. For our purposes, you can pretend it’s a positive value, which would then indicate the same relative performance we saw in the previous two charts.
Alpha
At this point the only metric we haven’t discussed is Alpha. Alpha is defined as the excess return earned above a specific benchmark (in this case, GLD).
What alpha attempts to do is answer the question: If an investment strategy experiences the same volatility (risk) as GLD, how much additional return would have been earned above what GLD delivered? In other words, did the investment strategy add value to what would have otherwise been achieved by simply investing in GLD?
We can see the alpha value for the GRM in the table below. Because GLD is the benchmark itself, it by definition has an alpha of zero.
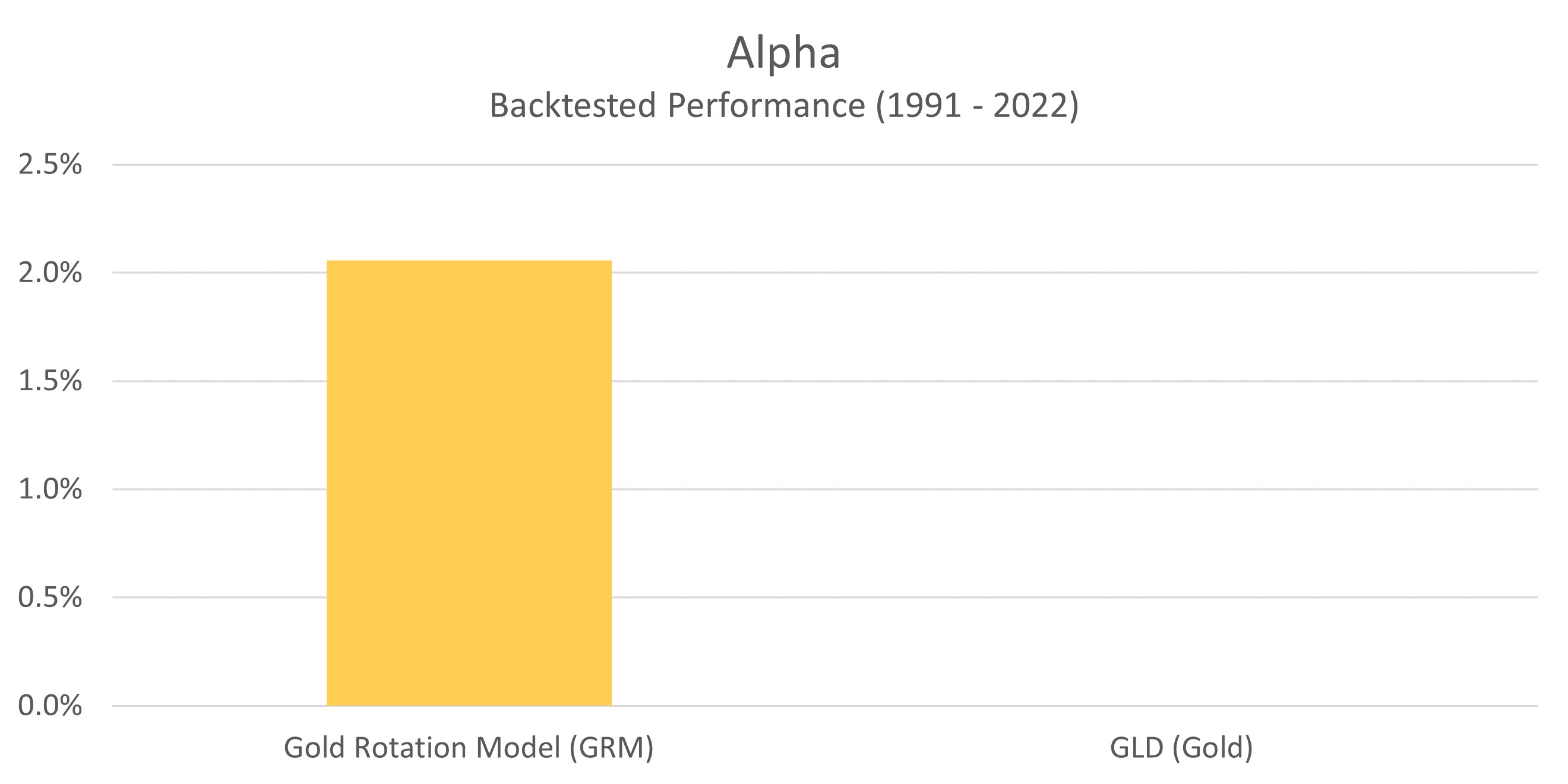
What this chart shows is that if the GRM had experienced the same amount of volatility as GLD (recall from our earlier charts that it experienced less), then the GRM would have earned an additional 2.06% per year above what GLD delivered. The reason this figure is higher than what we saw in the compound annual return chart is because once again, the GRM has experienced less overall risk. When we align the two portfolios to have the same risk characteristics, this is the hypothetical amount of outperformance that we would see.
Conclusion
When it comes to understanding the effectiveness of an investment strategy, the metrics we’ve outlined here are critical because they offer a complete picture of overall performance. Rather than focusing only on returns, as most investment managers do, we’ve lifted up our proverbial skirt to show you the risk that is inherent in our strategy as well. As a secondary benefit, this performance data also provides you with everything you would need to compare the GRM against other strategies in an apples to apples manner.
By taking the time to dig deeper into the GRM’s historical performance, we hope you’ve come away with a greater sense of why we believe it to be a much better alternative to a buy-and-hold approach to owning gold.
Find Out How to Use the GRM to Manage Your Investments


