Sign up for our Free Newsletter to access the best investment information money can’t buy.
The performance of an investment strategy can be measured using a series of basic financial metrics. These
industry-standard metrics allow investors to assess both the quality of returns, as well as the amount of risk that a
particular strategy has delivered.
We’ve summarized these performance metrics for our Sector Rotation Model (SRM) in the table below. However, unless you
happen to be a particularly savvy investor, there’s a good chance you have no idea what all these numbers mean. Not to
worry, in this section we’ll break down each of these metrics so that you can get a better understanding of the SRM’s
true capabilities.
| Sector Rotation Model (SRM) Performance Metrics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Strategy | Compound Annual Return | Alpha1 | Beta1 | Standard Deviation | Maximum Drawdown | Sharpe Ratio | Sortino Ratio | Treynor Ratio |
| SRM | 10.36% | 7.29% | 0.29 | 12.8% | -18.6% | 0.73 | 2.66 | 0.32 |
| SRM + ARM | 11.78% | 8.95% | 0.24 | 11.9% | -18.6% | 0.89 | 5.57 | 0.44 |
| SPY (S&P 500) | 6.95% | 0.00% | 1.00 | 18.3% | -50.8% | 0.38 | 0.43 | 0.07 |
| Data for 24-Year Period (2000 – 2023) 1 Benchmarked against the S&P 500 |
||||||||
The compound annual return is the rate of return that an investment strategy has achieved over time. It represents the
cumulative effect of a series of gains and losses on an original amount of capital. In the chart below, you can see that
both the SRM and SRM + ARM have delivered significantly higher returns than the overall stock market.
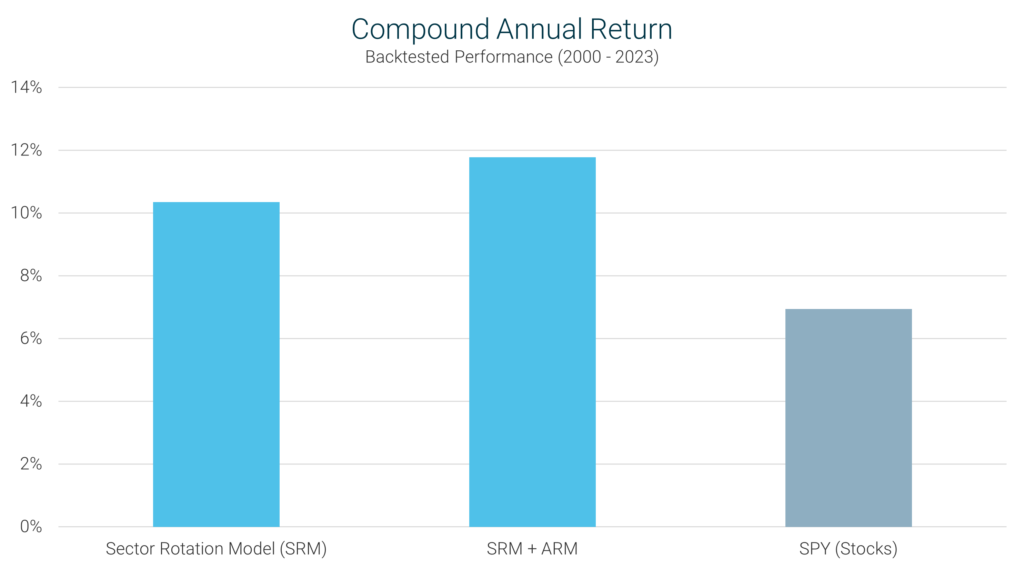
The outperformance that you see here is the result of two primary factors. First, because certain sectors of the market
are always outperforming others, returns can be enhanced by focusing on the sectors that are performing the strongest.
In addition, the SRM, like all of our models, has a built-in mechanism for moving to cash during severe market declines.
By limiting losses during these treacherous periods, the SRM is able to hold on to a larger portion of its gains.
The difference in performance that you see between the SRM and SRM + ARM is simply the result of investing in bonds (per
the ARM’s recommendation) rather than cash, when the SRM is out of the stock market. As you can see, this provides a
substantial benefit.
Not only has the SRM vastly outperformed the overall stock market, it has done so while exposing the portfolio to less
risk. We can see this by examining the three primary metrics that are used to quantify risk: standard deviation, maximum
drawdown, and beta.
Standard deviation is the most common measure of risk used in the financial industry. It measures the variability of
returns over time. The lower the standard deviation, the more consistent the returns are, and therefore the more “safe”
a particular strategy is. A higher standard deviation, on the other hand, implies that returns fluctuate wildly from one
year to the next.
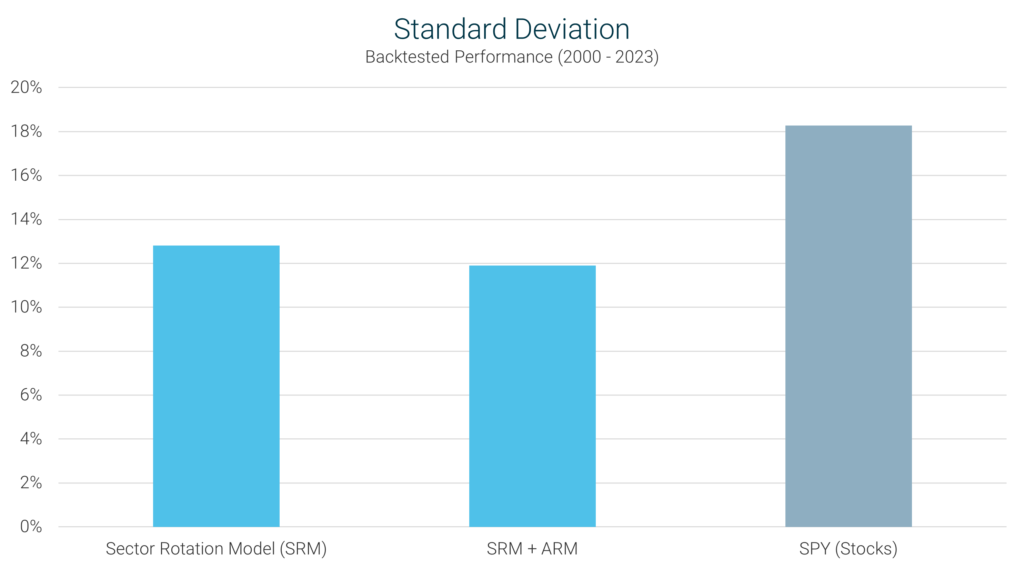
In this chart we can see that the SRM only experiences about 75% of the volatility of the broader stock market, with the
SRM + ARM experiencing slightly less. In other words, the SRM’s portfolio is exposed to approximately 25% less overall
risk than the market. That’s very significant.
In order to understand the benefit of this lower volatility, we need to see how volatility can translate into big
losses. We’ll do this in the next section.
Maximum drawdown is one of the more intuitive ways to measure risk. It looks at the biggest peak-to-trough decline that
an investment strategy has ever experienced. It should come as no surprise that the smaller the maximum drawdown, the
better. We can see maximum drawdowns for the SRM as well as the overall market in the chart below.
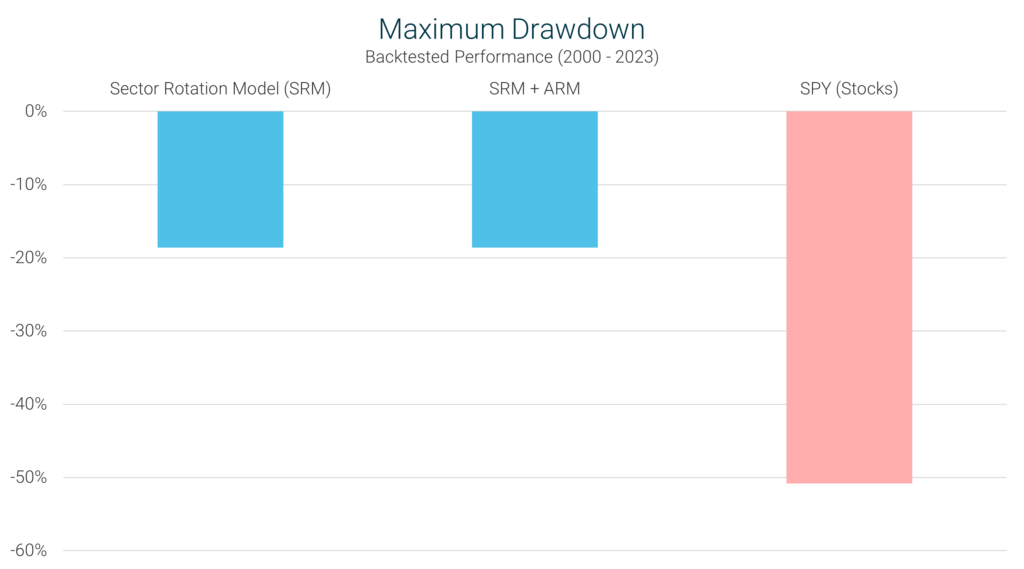
Notice that stocks, as measured by the S&P 500, have experienced drawdowns in excess of 50%. This has actually occurred
twice over the last two decades, during the dot-com collapse and again during the financial crisis. The SRM, on the
other hand, was able to recognize deteriorating conditions during these treacherous periods and moved the entire
portfolio to cash (or bonds in the case of the SRM + ARM). As a result, the most the SRM has ever fallen from
peak-to-trough is 18.6%. For the SRM + ARM, the maximum drawdown is also 18.6%.
This chart presents one of the most compelling arguments for using the Sector Rotation Model. By now you should be able
to recognize that the SRM allows you to participate in more upside than a 100% stock portfolio can deliver, but also be
exposed to significantly less downside risk.
Now let’s take a look at our last measure of risk: beta.
Beta measures the volatility (risk) of an investment strategy relative to the S&P 500. A beta of 1 implies the same
level of volatility as the S&P 500, while a beta less than 1 implies less risk, and a beta greater than 1 implies more
risk. Once again, we can see in the chart below that market risk for the SRM is significantly lower than that of the
broader market.
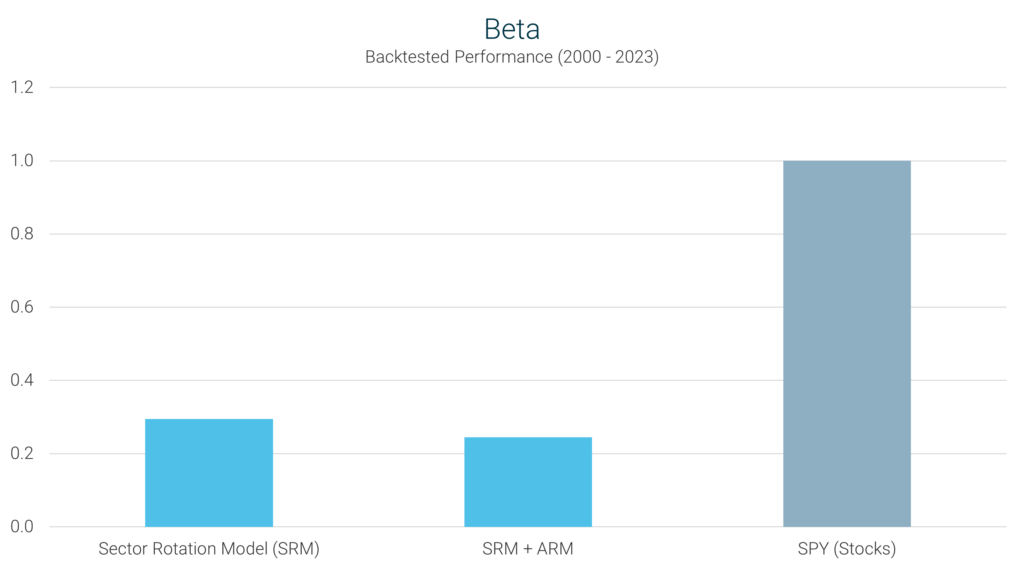
In this chart, SPY represents the S&P 500, so it has a beta of 1. The Sector Rotation Model has a beta of 0.32, which
means it only experiences 32% of the volatility of the broader stock market. The SRM + ARM’s beta is even lower at 0.27,
indicating even less risk with respect to the S&P 500. This is again due to having the portfolio in bonds rather than
cash when the SRM has exited the market.
Now that we’ve covered the metrics that identify both risk (standard deviation, maximum drawdown and beta) as well as
returns (compound annual return), we can combine these measures to get a better understanding of risk-adjusted returns.
This is considered the holy grail of investing because it represents how efficiently capital is deployed. Anyone can
increase returns by taking on more risk, but great investment strategies deliver high returns while taking less risk.
The Sharpe ratio is the industry standard method for measuring risk-adjusted returns. It looks at the excess return
earned in relation to the standard deviation (or volatility) of those returns. With Sharpe ratios, a higher number
reflects greater risk-adjusted returns (a good thing).

Here we can see that both the SRM and SRM + ARM are able to deliver substantially higher risk-adjusted returns than the
overall market. This is accomplished by not only earning higher returns (as we saw from the compound annual return
chart) but also doing so while exposing the portfolio to less risk (as we saw in the previous three charts). Based on
the data above, we can say that the SRM earns nearly twice the return per unit of risk as the general stock market.
When it comes to deciding how to invest, Shape ratios are an extremely important consideration because they demonstrate
the true effectiveness of an investment strategy. Looking at returns alone can be misleading because you have no idea
how much risk was taken to achieve those returns. The Sharpe ratio illuminates this important information, and gives you
a complete picture of the risk-reward profile.
The Sortino ratio is another measure of risk-adjusted returns that is very similar to the Sharpe ratio. However, instead
of comparing returns against the total volatility of a portfolio, it compares returns against only the downside
volatility (or risk). The assumption here is that volatility to the upside (higher than expected returns) is a good
thing, and therefore shouldn’t be penalized.
As with the Sharpe ratio, higher values here represent more effective use of capital.
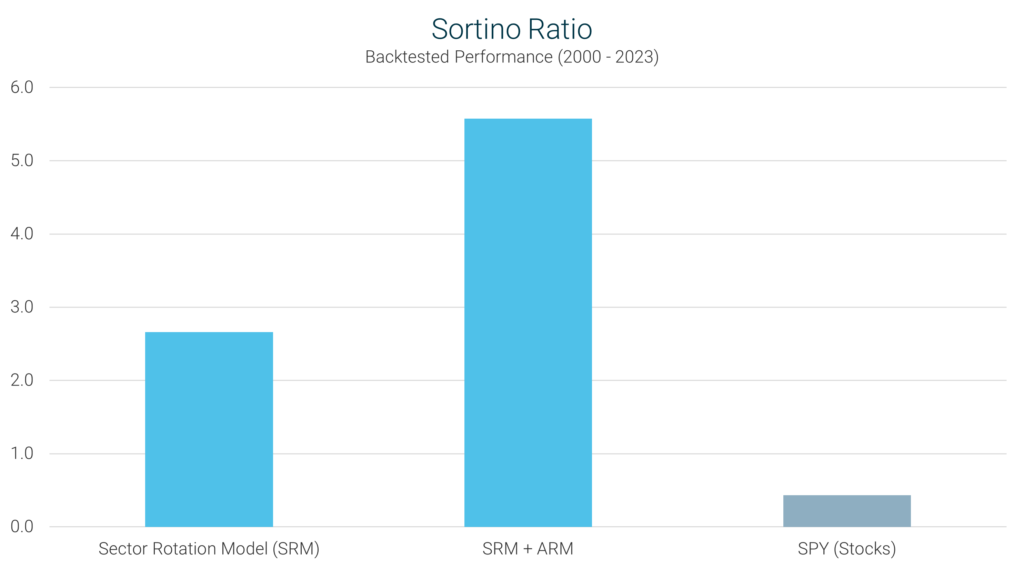
Once again, we can see that the SRM is able to generate significantly higher returns per unit of risk than the broader
market. The relative outperformance here is more substantial than with the Sharpe ratio because of the fact that upside
volatility is not penalized. This means that a significant portion of the SRM’s (and SRM + ARM’s) volatility comes from
better than expected returns, as opposed to worse than expected returns.
The last measure of risk-adjusted returns that we’ll look at is called the Treynor ratio, and like the previous two
metrics we examined, higher values are better. In this case, the measure of risk used is beta. So we’re looking at the
excess returns achieved with regard to overall volatility in relation to the S&P 500.
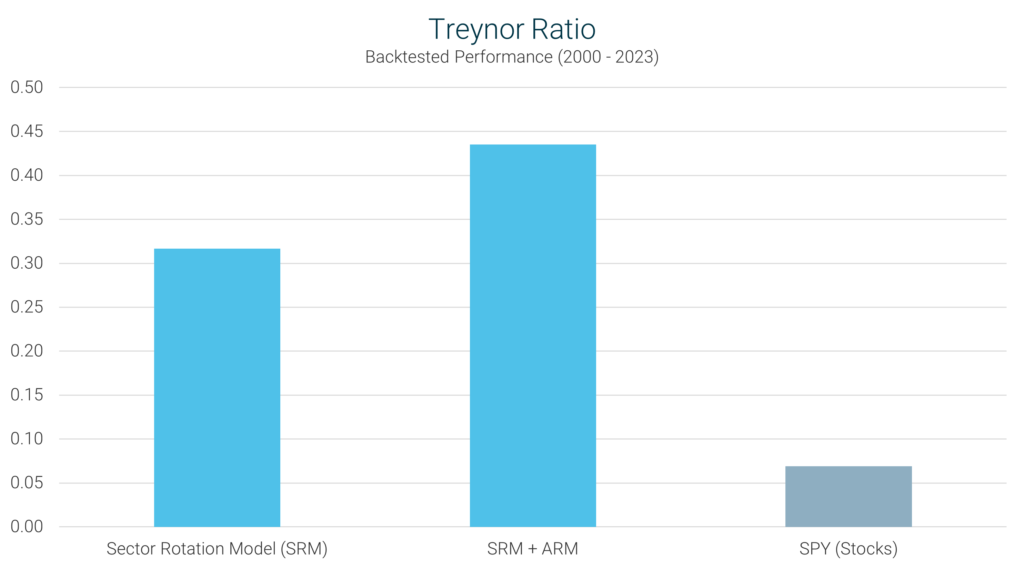
As you can see, the message here is the same. Both the SRM and SRM + ARM have significantly outperformed the market in
terms of risk-adjusted returns. The dramatic outperformance here is a result of the low betas that we saw earlier. By
achieving higher returns on much lower volatility (in relation to the S&P 500), the SRM exhibits a much more effective
use of capital.
At this point the only metric we haven’t discussed is Alpha. Alpha is defined as the excess return earned above a
specific benchmark (in this case, the S&P 500).
What alpha attempts to do is answer the question: If an investment strategy experiences the same volatility (risk)
as the S&P 500, how much additional return would have been earned above what the S&P 500 delivered? In other words, did
the investment strategy add value to what would have otherwise been achieved by simply investing in an S&P 500 index fund?
We can see the alpha values for our three portfolios below.
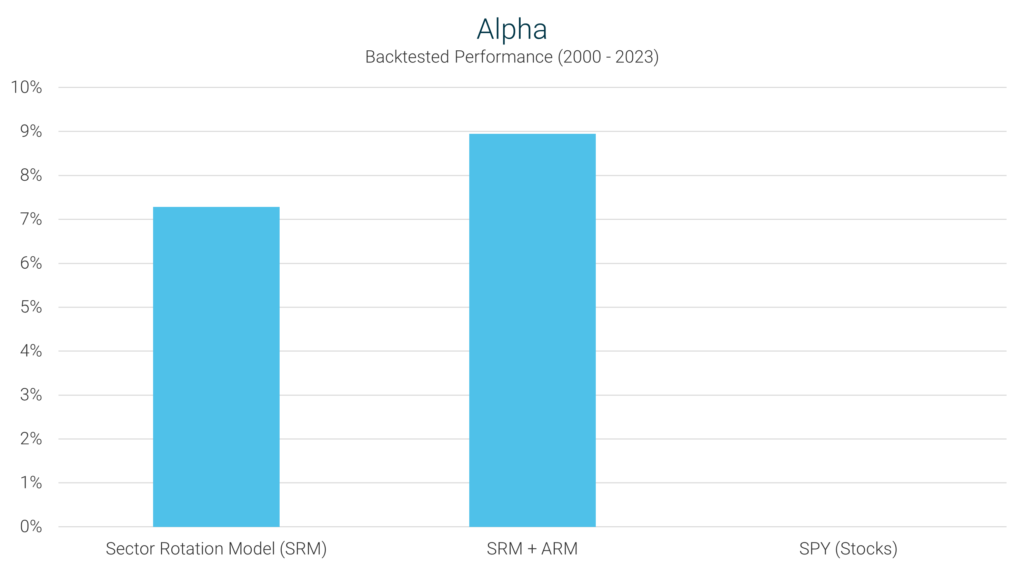
What this chart shows is actually quite eye-opening if you understand the data. It tell us that if the SRM had
experienced the same amount of volatility as the S&P 500 (recall that it had a beta of 0.32, meaning it only experienced
32% of the volatility of the S&P 500), it would have earned an extra 7.74% per year above what the S&P 500 delivered.
The outperformance is even greater for the SRM + ARM, due both to its higher returns, as well as an even lower beta
(0.27). If the SRM + ARM’s volatility were scaled up to match that of the S&P 500, it would have earned 9.35% more per
year than the index.
When it comes to understanding the effectiveness of an investment strategy, the metrics we’ve outlined here are critical
because they offer a complete picture of overall performance. Rather than focusing only on returns, as most investment
mangers do, we’ve lifted up our proverbial skirt to show you the risk that is inherent in our strategy as well. As a
secondary benefit, this performance data also provides you with everything you would need to compare the SRM against
other strategies in an apples to apples manner.
By taking the time to dig deeper into the SRM’s historical performance, we hope you’ve come away with a greater sense of
why we believe it to be an excellent supplemental strategy to an already diversified portfolio.
For instructions on how to use the ARM, please see the tutorial
Find out more about the cost of membership
The information provided here is for informational purposes only. Model
returns do not reflect
any management fees,
transaction costs or expenses. Investing involves a great deal of risk, including the loss of
all or a portion of your investment.
Nothing contained herein should be construed as a warranty of investment results. Past
performance is not an indication of
future results. All risks, losses and costs associated with investing, including total loss of
principal, are your responsibility.
Model Investing maintains positions in the funds discussed within this site according to model
recommendations.
