Sign up for our Free Newsletter to access the best investment information money can’t buy.
The TSP Allocation Model (TSP Model) is designed to optimize the performance of Thrift Savings Plan accounts by dynamically adjusting allocations among the G, F, C, S, and I funds based on prevailing market conditions. Unlike traditional static investment strategies, the TSP Model actively reallocates assets to capitalize on growth opportunities during economic expansions and to preserve capital during downturns.
To assess its effectiveness, we compare the TSP Model’s performance against several benchmarks, including the C Fund (S&P 500), the F Fund (Bonds), and a traditional 60/40 stock-bond portfolio.
The table below presents key performance metrics over a 23-year period (2002–2024), providing insights into return potential, volatility, and risk-adjusted performance. Each metric is analyzed in detail to illustrate how the TSP Model outperforms conventional investment strategies.
| TSP Model Performance Metrics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Strategy | Compound Annual Return | Alpha1 | Beta1 | Standard Deviation | Maximum Drawdown | Sharpe Ratio | Sortino Ratio | Treynor Ratio |
| TSP Model | 10.18% | 4.66% | 0.48 | 11.4% | -22.8% | 0.81 | 1.87 | 0.19 |
| C Fund (S&P 500) | 9.46% | 0.00% | 1.00 | 18.0% | -50.9% | 0.53 | 0.66 | 0.10 |
| F Fund (Bonds) | 3.57% | N/A | 0.04 | 4.8% | -16.7% | 0.45 | 0.54 | N/A |
| 60/40 Stocks/Bonds | 7.85% | 0.89% | 0.64 | 11.8% | -29.5% | 0.59 | 0.77 | 0.11 |
| Data for 23-Year Period (2002 – 2024) 1 Benchmarked against the C Fund |
||||||||
Definition: The Compound Annual Return (CAR) represents the average annual growth rate of an investment over a specified period, assuming the reinvestment of profits. It provides a standardized measure to compare the performance of different investment strategies over time.
Interpretation: A higher CAR indicates a more robust growth trajectory, reflecting the strategy’s effectiveness in generating consistent returns. Investors often prefer strategies with elevated CARs, as they suggest efficient capital appreciation.
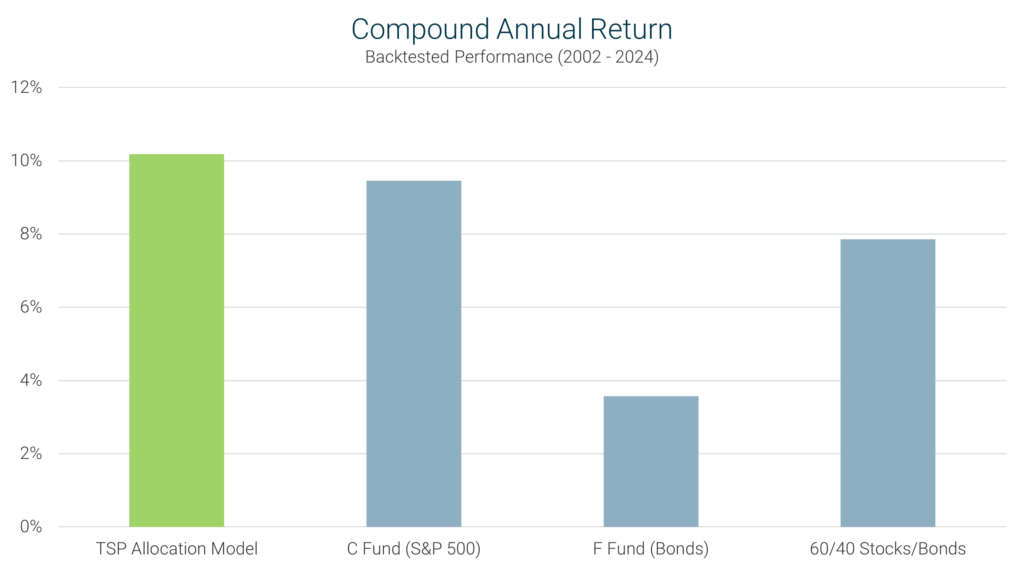
TSP Model’s Performance: Over the 23-year period from 2002 to 2024, the TSP Model achieved a CAR of 10.18%, outperforming the C Fund’s (S&P 500) 9.46%. This performance underscores the TSP Model’s ability to dynamically allocate between funds, thereby enhancing overall portfolio growth.
Definition: Alpha measures the excess return of an investment relative to the return of a benchmark index, such as the S&P 500. It indicates the value that a strategy adds beyond market movements, adjusted for volatility.
Interpretation: A positive alpha signifies that the strategy outperforms the benchmark after accounting for volatility, while a negative alpha indicates underperformance relative to its volatility. An alpha of zero implies that the strategy performs in line with the benchmark, given its risk level.
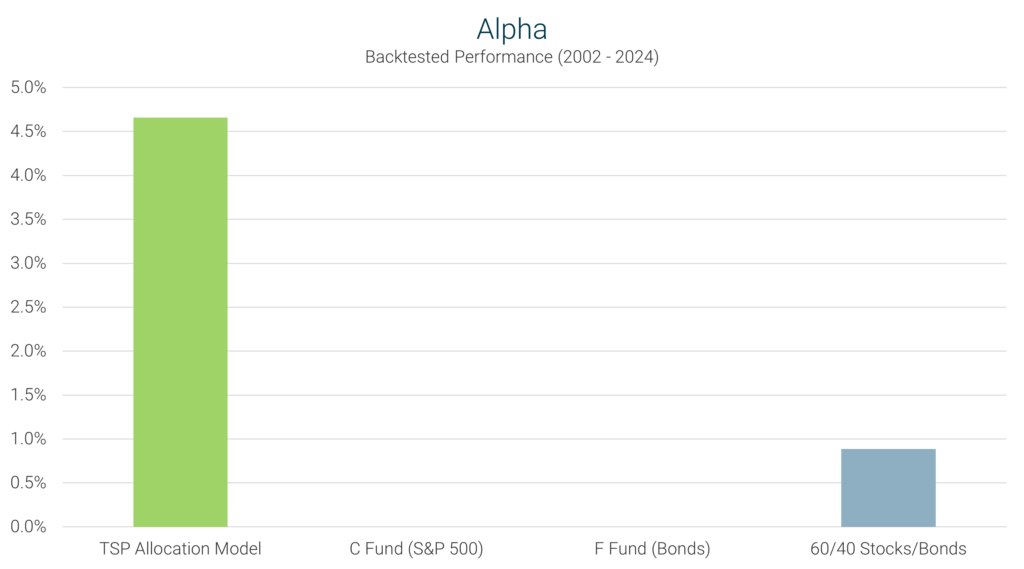
TSP Model’s Performance: The TSP Model recorded an alpha of 4.66%, indicating it delivered returns substantially above what would be expected based on its volatility. This positive alpha reflects the model’s proficiency in asset allocation and timing.
Definition: Beta measures how an investment’s returns respond to overall market movements. It quantifies the relationship between an asset’s price fluctuations and a benchmark index, such as the S&P 500.
Interpretation: A beta of 1.0 means the investment’s volatility mirrors the market. A beta greater than 1.0 suggests that the investment is more volatile than the market. Conversely, a beta less than 1.0 indicates that the investment is less volatile, offering more stability during market swings.
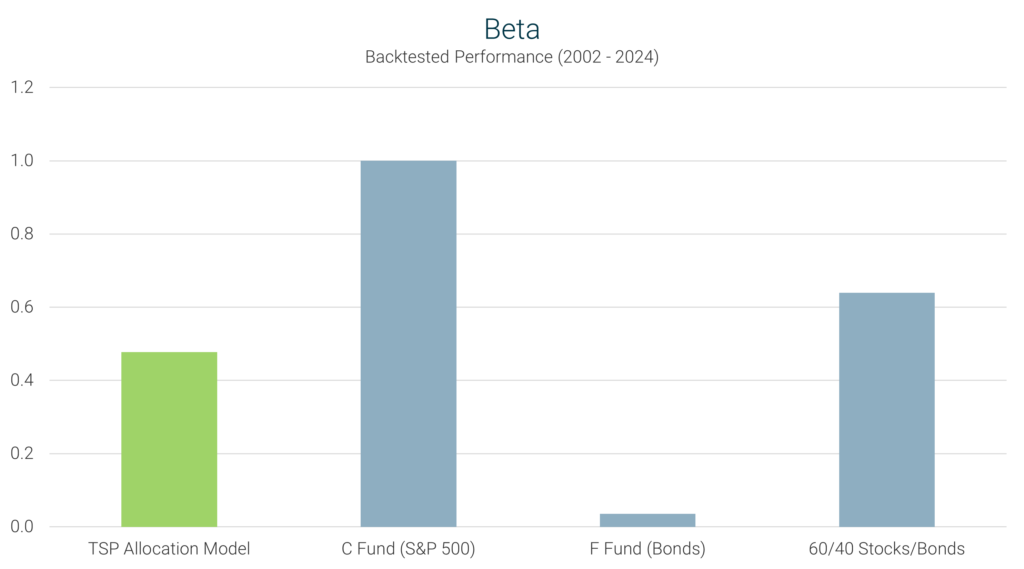
TSP Model’s Performance: With a beta of 0.48, the TSP Model exhibits significantly lower sensitivity to market movements compared to the C Fund’s beta of 1.0. This reduced beta indicates that the model is less affected by market volatility, contributing to a more stable investment experience.
Definition: Standard Deviation quantifies the dispersion of an investment’s returns around its mean. A higher standard deviation indicates greater variability in returns, signifying higher risk.
Interpretation: Investors seeking stability and growth prefer strategies with lower standard deviations, as they offer more predictable returns.

TSP Model’s Performance: The TSP Model’s standard deviation is 11.4%, which is lower than the C Fund’s 18.0%. This suggests that the model provides a more consistent return pattern, reducing the uncertainty associated with investment outcomes.
Definition: Maximum Drawdown measures the largest peak-to-trough decline in an investment’s value over a specified period. It reflects the most significant loss an investor could experience before a recovery to the previous peak.
Interpretation: A smaller maximum drawdown is preferable, as it indicates the strategy’s effectiveness in preserving capital during market downturns.

TSP Model’s Performance: The TSP Model experienced a maximum drawdown of -22.8%, significantly less severe than the C Fund’s -50.9%. This demonstrates the model’s capability to mitigate losses during adverse market conditions.
Definition: The Sharpe Ratio measures an investment’s return relative to its total risk, as indicated by standard deviation. It provides insight into how efficiently a strategy converts risk into returns and helps investors compare different investment options based on their risk-adjusted performance.
Interpretation: A higher Sharpe Ratio indicates that the strategy is generating better returns per unit of risk taken, making it more efficient. A lower Sharpe Ratio suggests that the strategy may not be utilizing market exposure as effectively.
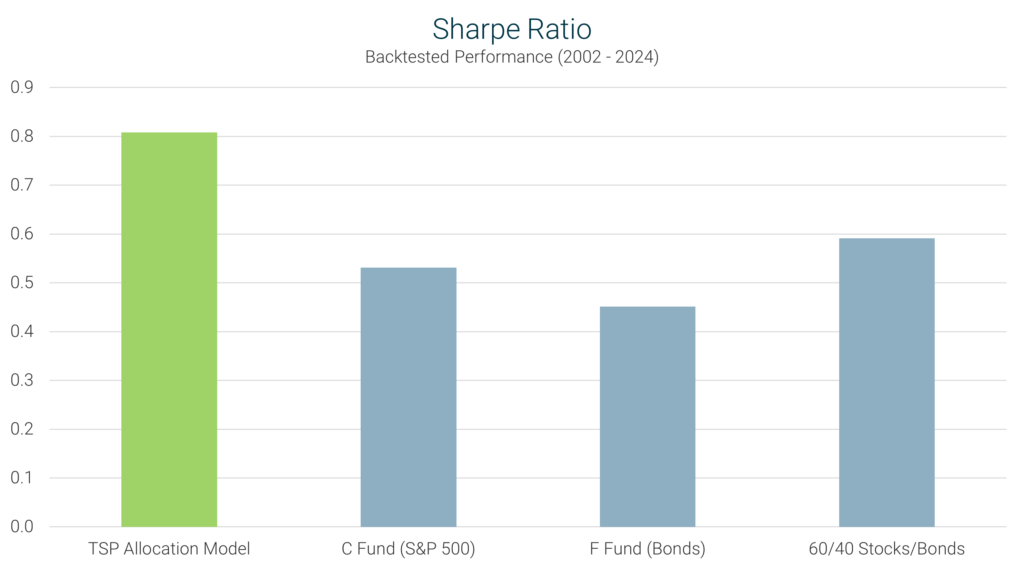
TSP Model’s Performance: The TSP Model achieved a Sharpe Ratio of 0.81, outperforming the C Fund’s (S&P 500) ratio of 0.53. This confirms that the TSP Model delivers superior returns while maintaining lower overall risk, making it a more stable and efficient investment approach for Thrift Savings Plan participants.
Definition: The Sortino Ratio is a variation of the Sharpe Ratio that focuses solely on downside volatility, excluding the impact of positive returns. It measures the return of an investment relative to the risk of negative returns.
Interpretation: A higher Sortino Ratio indicates that a strategy is effectively generating returns while minimizing exposure to downside risk. Conversely, a lower Sortino Ratio suggests that the strategy may be more susceptible to negative returns.
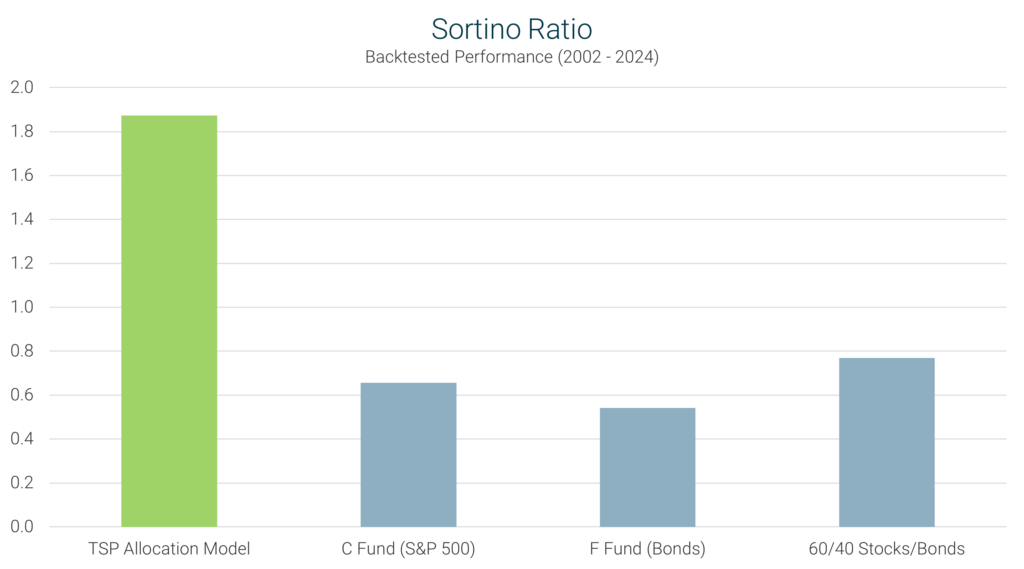
TSP Model’s Performance: The TSP Model achieved a Sortino Ratio of 1.87, significantly outperforming the C Fund’s (S&P 500) ratio of 0.66. This demonstrates the model’s proficiency in delivering strong returns while effectively managing downside risk.
Definition: The Treynor Ratio evaluates an investment’s returns relative to its exposure to systematic market risk, as measured by beta. It assesses how well the strategy compensates investors for taking on market risk.
Interpretation: A higher Treynor Ratio indicates more efficient use of market risk, with higher returns per unit of market risk assumed. A lower Treynor Ratio suggests less efficient utilization of market risk, with lower returns for the level of market risk taken.
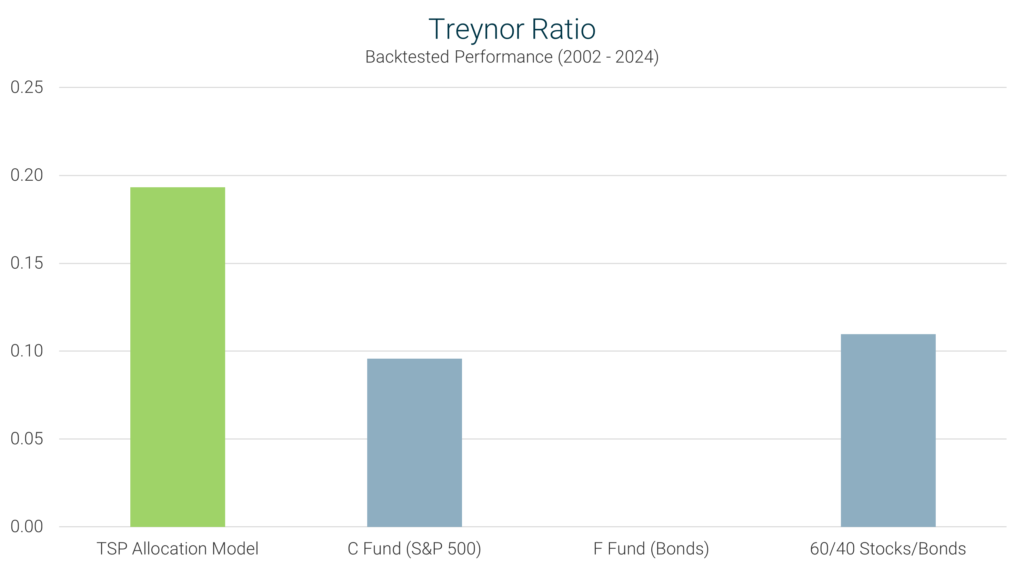
TSP Model’s Performance: The TSP Model recorded a Treynor Ratio of 0.19, outperforming the C Fund’s (S&P 500) ratio of 0.10. This reflects the model’s superior efficiency in converting market risk into returns.
The TSP Allocation Model (TSP Model) has demonstrated exceptional performance across key investment metrics, making it an ideal choice for Thrift Savings Plan participants.
By actively adjusting allocations among the G, F, C, S, and I funds based on market conditions, the TSP Model captures growth opportunities during economic expansions while preserving capital during downturns. It represents a vast improvement to conventional buy-and-hold TSP investment approaches.
For federal employees and service members seeking to maximize their retirement savings, the TSP Model offers a sophisticated yet practical strategy that aligns with the dynamic nature of financial markets, ensuring a more secure and prosperous financial future.
Optimize your TSP today – sign up and start your free trial!
Sign Up Now for Access to the TSP Allocation Model!
The information provided here is for informational purposes only. Model returns do not reflect any management fees, transaction costs or expenses. Investing involves a great deal of risk, including the loss of all or a portion of your investment. Nothing contained herein should be construed as a warranty of investment results. Past performance is not an indication of future results. All risks, losses and costs associated with investing, including total loss of principal, are your responsibility. Model Investing maintains positions in the funds discussed within this site according to model recommendations.
